Angular Momentum and Its Law of Conservation and Fundamentals
Imagine a figure skater, moving on an ice beautifully and smoothly. As they pull down their arms, an enchanting thing—An online spin becomes even faster as if they are not adherent to the law of gravitation. Testifying to the ability of angular momentum to mesmerize, this is a fascinating phenomenon indeed.
What is Angular Momentum?
While linear momentum refers to objects’ ability or desire to move in a direct line, angular momentum has a similar inclination in describing objects’ desire to rotate. It is the rotational equivalent of linear momentum and is present everywhere in the universe ranging from the sub-atomic particles to galaxies.
Importance and Applications: Angular momentum is one of the fundamental concepts of physics and is used to explain things such as the motion of planets and rotating black holes, as well as atomic structure. It’s also at the center of engineering as it is responsible for the operations of gyroscopes, and efficiency of flywheels and dexterity of robotic arms.
Understanding the Fundamentals
Angular Momentum of a Point Particle:
Let us think of a particle that moves in a circular motion and is confined in a location of specific radius. Its angular momentum (denoted by the symbol “L”) is determined by three key factors:
Moment of Inertia (I): This refers to how the object opposes any alteration in its state of rotary motion. It depends on the mass which the particle has as well as distance from the axis of rotation. It is similar to mass but rotated with time instead.
Angular Velocity (ω): This tells us the rate of rotation of the particle. It simply refers to the angular velocity, or the rate at which the object is spinning in radians per second.
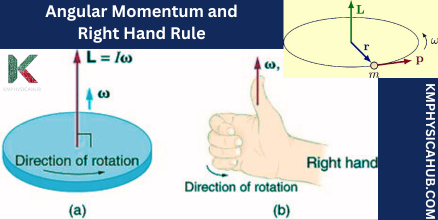
The Right-Hand Rule: Angular momentum like linear momentum is also a vector physical quantity, it shall be described by the magnitude as well as direction. The direction is determined by the right-hand rule: This is the direction of rotation; if you clench your fingers in the direction of rotation, the thumb will point in the direction of the vector.
For the case of a point mass, we have the following expression L = Iω
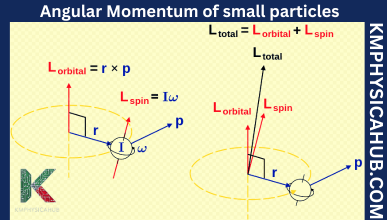
Angular Momentum of Rigid Bodies:
For the rest let us be more precise and apply it to objects which are rigid, like a spinning top, planets or human creatures. In the case of the rigid body, an additional factor called the moment of inertia is a bit more elaborate and determined by the geometry of the body and its mass distribution. For instance, a long point like a rod is different from the moment of inertia from a sphere with an equivalent mass.
Conservation of Angular Momentum: This is where things are getting a lot more intriguing! This means that in a closed system in which no external torques act angular momentum is conserved or calculated as the sum of the moments of inertia. This fundamental principle explains why our figure skater spins faster when they pull their arms in: it lowers their moment of inertia, then their angular velocity have to increase to maintain the same angular momentum.
Applications in Physics and Astronomy: From Planets to Black Holes
Planetary Motion and Kepler’s Laws:
The planets of our solar system also rotated nicely around Sun in sheer ballet like motion, under the control of Kepler’s laws. These laws can be derived from the fact that the total angular momentum of a system is conserved. The angular momentum of a planet remains constant through its orbital path and consequently, a planet will move faster when it is closer to the Sun and its moment of inertia is smaller and slower when it is farther away from the Sun.
Rotating Black Holes and Accretion Disks:
Even something as hard to comprehend as a black hole is not an exception to angular momentum laws. When matter approaches a black hole, it starts orbiting in a spinning manner hence forms a disk of intense heated gas known as an accretion disk. Angular momentum explains how the disk rotates and is the main factor affecting the black hole mass and its development.
Atomic and Nuclear Physics:
Zoom down to the quantum realm, and you’ll find angular momentum playing a pivotal role in the structure of atoms themselves. Electrons, those tiny particles whizzing around the nucleus, possess an intrinsic angular momentum called “spin.” This spin, quantized and unchanging, determines an electron’s magnetic properties and governs how atoms interact with each other.
Angular Momentum in Engineering: From Navigation to Robotics
Gyroscopes and Inertial Navigation:
How about the example of the spinning skater? A gyroscope works on the same principle! Similar to the skater, a spinning gyroscope will not allow changes to occur to it relatively to its orientation as a result of the principle of conservation of angular momentum. This unique characteristic of gyroscopes renders them extremely useful in especially navigation. Gyroscope is somewhat like a mini-compass that gives a steady course when directions may be unpredictable like in airplanes, ships as well as spacecrafts. They are the unspeaking pilots, steering us through the flight and over the deep.
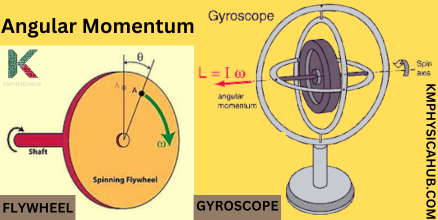
Flywheels for Energy Storage:
A heavy wheel with many blades spinning round—there is stored energy, a supply of kinetic energy in it! In the operational categories, flywheels take advantage of the principle of angular momentum to store energy mechanically. Energy is constantly supplied to the flywheel and it starts rotating faster and the added energy is converted to special energy known as kinetic energy of rotation. This stored capacity can again be discharged according to the requirements of electrical energy and can supply a surge of power when required. Applications of flywheels include use in electrical network fluctuations, force storage and regenerative braking in HEVs.
Robotics and Control Systems:
Navigating a robot to move with smooth and elegance is not an easy process and for this the concept of angular momentum is very important. With robotic arms for instance, one has to come up with sophisticated models in the control of their motion in terms of angular momentum of the joints and link. Currently, engineers, through complex control equations, are able to design and develop robots that would be able to grasp and relate to objects with ease and flexibility as living beings.
Angular Momentum in Everyday Life and Sports
Angular momentum is not confined to textbooks and laboratories—it’s the unseen force behind many of our everyday experiences:
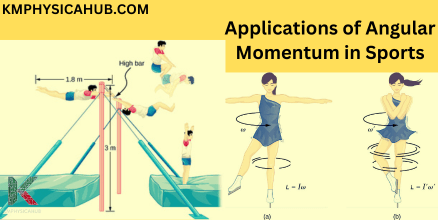
Sports Applications:
Quite unconsciously, athletes are renown for their skills in maneuvering angular momentum. This principle comes into play when a figure skater pulls the arms in to spin faster, a diver taking their legs in to do breath-taking revolutions, a gymnast to gain maximum spin over the uneven bars. They know, on the basic level of instinct, that the moment of inertia has an impact on the angular velocity.
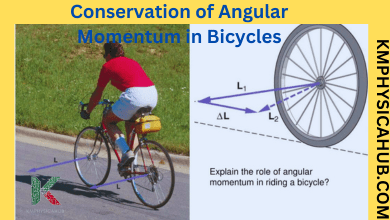
Bicycles and Motorcycles:
Have you ever asked your self how these tiny creatures manage to stand straight? Angular momentum has its use! The wheels of a bicycle or a motorcycle have a tendency to maintain their orientation or position similar to that of gyroscopes. This gyroscopic effect works to stabilize the motorcycle, to the extent that at low speeds, the machine can be more stable than its rider. When the wheels turn faster, it creates more angular velocity and this in turn makes the vehicle more rigid. It has got to do with gravity, mass and angular velocity and much of the time it is a balancing act.
Simple Toys:
Most basic toys can be a great show of scientific principles! A spinning top always appears to be balanced on its point, its twirling which is quite fascinating is related to the law of conservation of angular momentum. A yo-yo moving up and down the string and coming back with a spin highlights the principle of straight and rotary movement.
Advanced Concepts: Delving Deeper into the World of Spin
Torque and Angular Acceleration:
Torque is defined as the rotational force also known as the moment of a force. This is closely connected with angular momentum by means of angular acceleration (α) – it describes how rapidly if at all the object rotates. Just as force is related to linear acceleration through Newton’s second law (F = ma), torque (τ) is related to angular acceleration through the rotational equivalent: τ – Iα In other words, torque determines how the object’s angular momentum is either gained or lost.
Precession and Nutation:
Can you ever watch a top or a pin spinning round the table and as it gradually slows down, it begins to sway from side to side? This interesting occurrence is called precession, and this is due to the way the top rotates based upon angular momentum as well as the torque created by gravity. Additionally, instead of just toppling over and rolling, the axis of rotation of the top gradually changes, describing a cone-like motion. Another kind of movement related to top is nutation which adds a slight rocking motion to the precessional motion making the top again to move in a more complicated and interesting manner.
Conclusion:
Angular momentum is a concept, which has its usage in a broad context of scientific curriculums. It plays a part in assisting the design and function of mechanical systems, helps explain celestial mechanics, and is used to shape human motion in athletics. Present day research still goes further ahead trying to explain with more precision on the issues of angular momentum from issues as simple as the behavior of super fluids to as complex as rocket science and this is why the study is important.
FAQs
Q1. What is angular momentum?
A: The quantity of rotation exhibited by an object is referred to as angular momentum. Angular momentum is a relative of linear momentum but in the angular setting.
Q2. What factors determine angular momentum?
A: Angular momentum depends on moment of inertia, angular velocity, and the axis rotation of an object.
Q3. State the law of conservation of angular momentum?
A: Sum of angular momenta in a closed system is conserved or is constant or remains the same during a process. This means for instance that if an object’s moment of inertia changes, the angular velocity accompanying the object must change to balance the overall angular momenta.
Q4. How does angular momentum apply to figure skating?
A: A figure skater spins faster when pulling their arms in because they decrease their moment of inertia and increase their angular velocity so that their total angular momentum remains constant.
Q5. How does angular momentum work in gyroscopes?
A: Gyroscopes take advantage of the principle of no changes in angular momentum to provide resistance to certain orientations. They do not easily roll or balance which makes them suitable for use in areas that require navigation such as roads.
