What is Projectile Motion?

Picture this: when you tie a rod and you have a ball at the other end and you release it, it moves in a graceful parabolic path and then descends to the ground. Now that is projectiles in motion! It’s the motion where an object is moving in two dimensions only under the force of gravity for which we tend to ignore the factor of air resistance.

The Significance of Projectile Motion:

Since the times when ancient civilizations tried to aim at their enemies with arrows, or modern engineers try to launch rockets, projectile motion knowledge has always been essential. That makes it the basis of ballistics, sports science, every application in the military, and even computer animated movement in some movies!

Principles of Projectile Motion: 

Key Components:

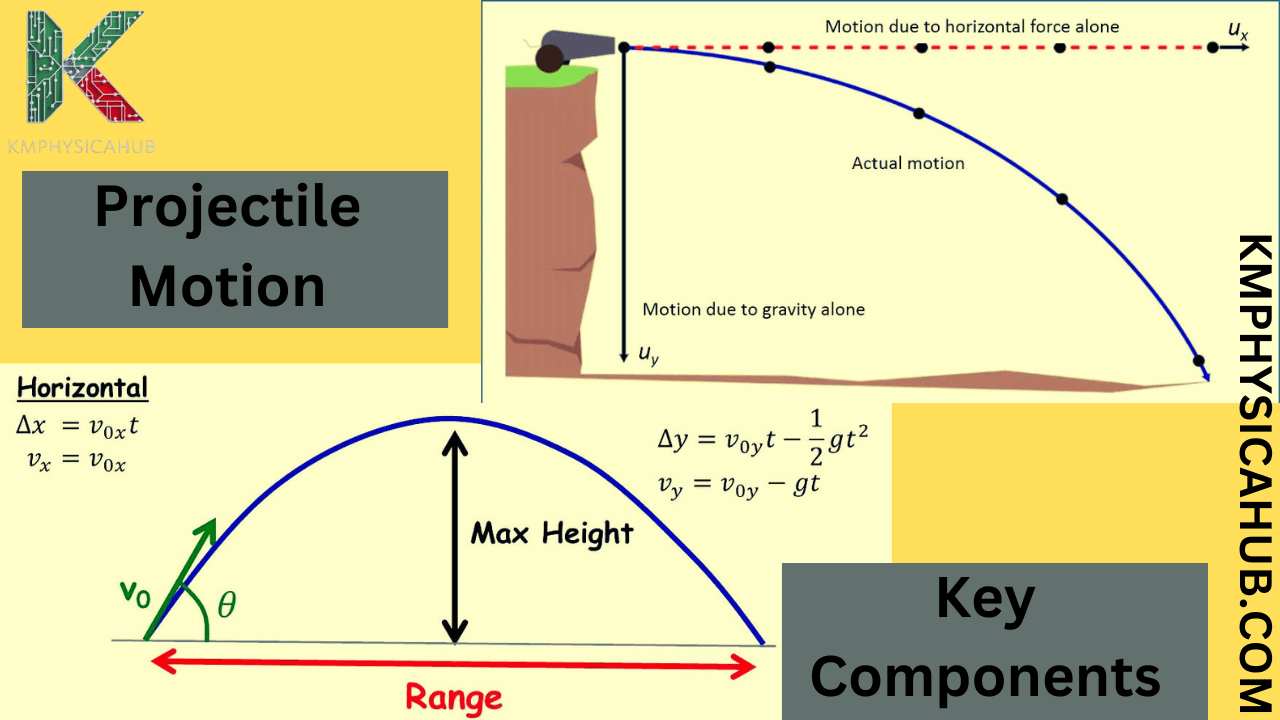
Trajectory: This is the term that is used to describe the curved pattern followed by a projectile. Often when thinking of projectiles, one would imagine an object moving through the air based purely on gravity; in this case, no matter the path of the initial angle the trajectory is always a parabola.

Initial Velocity (v₀): This is the velocity that the projectile has at the time when it is fired. One is the magnitude (speed), while the other is the direction which plays a very central role in defining the nature of the parabolic curve.

Launch Angle (θ): This is the position at which the projectile is fired or thrown in relation to the horizontal direction. It helps also in defining the range and maximum height of the projectile to reach.

Range (R): This is the total the projectile covers in the horizontal direction until it touches the ground.

Maximum Height (H): This is the highest position, it gets to before it starts to descend again during the flight cycle.

Time of Flight (T): This is total time taken in the flight of the projectile from the instance it was thrown until it lands on the ground.

Factors Affecting Projectile Motion:

Gravity (g): The most significant is a gravitational pull of the Earth which becomes a force that is responsible the falling curve of the trajectory.  It means the vertical velocity of the projectile undergoes changes of 9.8 meters per second every second, the acceleration due to gravity is about 9.8 m/s².

Air Resistance: This force of opposition to the motion of an object might encounter in a real scenario is called air resistance. The value of air resistance is defined by some conditions such as the projectile’s shape, size, and velocity.

Launch Conditions: The very first thing in the projectile path determining is initial velocity and the launch angle.  A higher initial velocity will result in a longer range, while the launch angle determines the trade-off between maximum height and range.

Mathematical Framework: Quantifying the Curves

Equations of Motion: The motion of a projectile is well explained using certain set of kinematics equations. These are equations that express relation between displacement of the projectile, its velocity, acceleration as well as time. Below are some formulas for projectile motion in two dimensions (horizontal and vertical):

• Horizontal Motion (assuming negligible air resistance):

Horizontal velocity remains constant:  vₓ = v₀ₓ 

Horizontal displacement:  x = v₀ₓt

• Vertical Motion:

Vertical velocity: vᵧ = v₀ᵧ – gt 

Vertical displacement: y = v₀ᵧt – (1/2)gt²

Where:

• x = horizontal displacement
• y = vertical displacement
• v₀ₓ = initial horizontal velocity
• v₀ᵧ = initial vertical velocity 
• vₓ = horizontal velocity at time t
• vᵧ = vertical velocity at time t
• g = acceleration due to gravity
• t = time

Worked Example:

Let an object is projected at an angle of 30° with respect to horizontal. Initial velocity of the object is 20m/s. We can use the equations above to calculate various parameters of its motion:

• Initial Horizontal and Vertical Velocities:

v₀ₓ = v₀cos(θ) = 20 * cos(30°) 

                      ≈ 17.32 m/s

v₀ᵧ = v₀sin(θ) = 20 * sin(30°) 

                     = 10 m/s

• Time of Flight (T):

This is total time taken in the flight of the projectile until it lands on the ground (y=0). We can use the vertical displacement equation and solve for t:

0 = v₀ᵧt – (1/2)gt²

0 = t(v₀ᵧ – (1/2)gt) 

This equation has two solutions: t = 0 (the initial moment) and t = (2v₀ᵧ)/g.  The second solution represents the time of flight:

T = (2 * 10 m/s) / 9.8 m/s²  

T  ≈ 2.04 s

• Maximum Height (H):

When the ball is at the highest point, the vertical velocity is zero (vᵧ = 0).  As we have the vertical velocity equation, we can use this to find the time it takes to reach this point and then substitute that time into the vertical displacement equation:

0 = v₀ᵧ – gt 

t = v₀ᵧ / g = 10 m/s / 9.8 m/s² 

               ≈ 1.02 s

Now, plug this time into the vertical displacement equation:

H = v₀ᵧt – (1/2)gt²

H = (10 m/s)(1.02 s) – (1/2)(9.8 m/s²)(1.02 s)² 

H  ≈ 5.1 m

• Range (R): 

Since the horizontal velocity remains constant (neglecting air resistance), we can simply multiply it by the time of flight to find the range.

R = v₀ₓT = (17.32 m/s)(2.04 s) 

             R ≈ 35.3 m

Applications of Projectile Motion:

Sports: 

The identification of projectile motion is central to many sports and acts as a soul to the extreme activity. Think of a baseball flying through the air, a basketball going through the hoop, or a golf ball arching perfectly to reach the green. In each case, athletes naturally understand the physics of projectile motion, using ranges, velocities of projection, and the orientations of rotation to attain the necessary results.

• For instance, each type of delivery in baseball whether a fastball, curveball, a slider, among others is arrived at by altering the release point and the throw and the precise flight path defined by physics of projectile motion.
• Same is with basketball players who have to remember the launch angle and force to get the ball flying just right through the hoop.
• The golfers study the ground and wind and to make the perfect arc of the shots one needs to adjust the technique of their hitting according to the distance that is required to be covered.

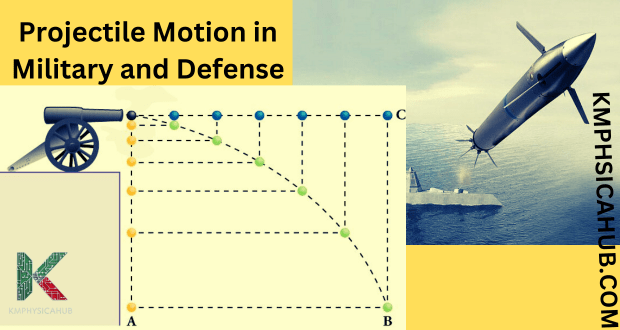
Military and Defense:

In the area of military and defense, projectile motion has a more significant sense or can be crucial. It is necessary to estimate accurately the motion properties of projectiles in order to apply it in artillery fire, missile launching and the like.

• Take for instance ballistics where professionals work hard to align launch velocities, angles, and other external parameters that relate to the trajectory of projectiles with the aim of delivering a blow on intended targets with a proper measure of impact while observing a maximum allowable level of collateral damage.
• In fact, much of the design of weapons systems relies directly on the concepts of projectile motion. Subsequently, aspects such as length of barrel, rifling (which comprises of grooves within the barrel), and projectile geometry are well planned in an attempt to enhance range and also ensure appropriate impact upon target termination.

Engineering and Technology:

Starting from simple applications as in the use of projectiles to setting up ramps, to complex applications such as in the planning of flight, projectile motion is utilized in a number of engineering disciplines.

• Water fountains, with their mesmerizing arcs of water, rely on precise calculations of projectile motion to create stunning visual displays. Engineers use their knowledge of launch angles, water pressure, and nozzle design to choreograph the water’s movement, transforming simple fountains into captivating works of art.
• Sprinkler systems, tasked with the important job of keeping our lawns lush and green, also depend on projectile motion. By carefully positioning sprinkler heads and adjusting water pressure, engineers ensure even water distribution across lawns and fields, maximizing coverage and minimizing waste.
• In the vast vacuum of space, flight and especially projectile motion is crucial for putting satellites in orbit and controlling them. The positions and velocities of everyone in satellite projects are calculated with great care, and factors such as the Earth’s gravitational force, speed of the satellite, and even effects from the gravitational pull of other bodies in the universe are considered. These calculations help put satellites into their intended orbits and perform their tasks effectively; whether they are employed in conveying information, positioning, or even research.

Applications of Projectile Motion at Home

• The Art of Tossing:

Throwing a Ball:

Whether it is a throw to a pet with a tennis ball, a friend with a frisbee or throwing socks into the laundry basket, every throw exemplifies projectile motion. This requires the coordination and dynamic control of the angle and force to bring it to the trajectory of the intended flight.

Serving a Volleyball:

From a simple game of volleyball in your own house to organizing a game online, it is all about learning from where to launch the ball, with what force and at what angle in order to get it land on the opponent’s side of the court.

Playing Catch:

Some more familiar examples include tossing a ball back and forth with your child or simply throwing the ball against the wall all of which illustrates basic projectile motion. You get to know how the ball is going to bounce, how to bend your throws and where it is going to land at.

• Kitchen Physics:

Tossing Food into the Microwave:

When you put a frozen dinner into the microwave and prepare to heat it, what you are doing is actually throwing an object. It normally requires tilting and pressing in a way so that it doesn’t splatter all over the place landing safely in the dustbin.

Pouring Liquids:

The simple task of pouring a glass of water or juice requires one to consider the liquid as a projectile upon being released. You tilt the pouring can in such a way that you are able to regulate the rate of flow so that you do not overflow the cups.

Flipping Pancakes:

One of the most famous tricks in cooking is the a flipping of a pancake, which involves the laws of physics of projectile motion. Flicking the righteous pancake, you estimate the height, velocity and spin to perfectly flip the pancake back into the pan without any comedy.

• Household Choreography:

Vacuuming Under Furniture:

To clean under a sofa or a bed, the nozzle is tilted appropriately to allow the suction head to get to the specific areas. It is like you are pointing a projectile (the nozzle of the vacuum cleaner) to suck away some matter in difficult areas.

Watering Plants:

When you are using a watering can to water your plants, you are in effect throwing an object – water. You can bend it to the required position that will allow the water to spray directly on the roots and with much force.

Throwing Away Trash:

Even the simple act of tossing a crumpled piece of paper into the trash bin involves basic principles of projectile motion. You calculate the angle and force needed to land the trash in the bin, avoiding a messy miss.

• The Wonders of Water:

Taking a Shower:

Another perfect example of multiple projectiles is the visualization of a showerhead where numerous drops of water are released in multiple directions. It is a mechanism that you move with an aim of directing the flow of the water in the direction you want or may be increasing or reducing the force with which water is being sprayed.

Filling a Bathtub:

The water that pours from the faucet into the bathtub has a trajectory of a projectile. You turn the handle that regulates the flow of water into the tub so that it fills with a moderate rate.

• The Everyday Tools of Projectile Motion:

Using a Slingshot:

Looking even at a simple object like a slingshot makes one understand how theories and principles of projectile motion work. You take a stone or a small object and firmly fix it into the two elastic ropes of the slingshot and then aim at the desired path.

Playing Darts:

Some of the concepts of projectile motion are employed in the act of taking a dart and aiming at the target. Even though this move is almost similar to the first one, you have to change the angle and force to get the trajectory that will enable you land the dart in the bullseye.

Advanced Concepts:

Air Resistance:

However, we normally depict projectile motion as if there is no air resistance, despite the fact that the force will inevitably affect the projectile path particularly where distances are large or velocities high.

 

• A force called air resistance or drag opposes the direction of motion by slowing down the projectile and thus shortening the range. Air resistance varies in proportion to such parameters as the shape, size and speed of the projectile, as well as density of the air.
• A skydiver for instance could be considered. Air resistance increases as the skydiver falls because air acts on the object proportional to its velocity. Finally, the air resistance becomes equal to the force of gravity. After that the skydiver moves at terminal velocity (constant speed).

Parabolic vs. Non-parabolic Trajectories:

While the classic depiction of projectile motion involves a graceful parabolic arc, real-world scenarios often introduce complexities that can lead to deviations from this idealized path.

• Factors like wind, air resistance (as discussed earlier), and variations in gravitational pull can all contribute to non-parabolic trajectories. For instance, a projectile launched in a strong tailwind might travel farther than expected, while a headwind could significantly reduce its range.
• Under certain circumstances, for example when the direction of the projectile is intercontinental, the semicircle curvature of the Earth also becomes a factor, and much of the path is elliptical.

Conclusion

This simple idea of projectile motion contains the degree of complexity capable to explain the behavior of a vast number of things in our world: be it toys that children toss in a play or the wings of technologies that save human lives. The more we explore the finer details of projectile motion the more we able to discover ways to enhance science in various fields such as sporting activities, military and aerospace engineering.

People Also Ask

Q1. What is projectile motion?

A: Projectile motion is the curved path an object follows when launched into the air, influenced only by gravity (and sometimes air resistance).

Q2. Give 5 everyday examples of projectile motion?

1. Throwing a ball
2. Pouring a glass of water
3. Vacuuming under furniture
4. Taking a shower
5. Playing darts

Q3. What is the Coriolis effect?

A: The Coriolis effect is basically the deviation of a projectile when fired because of the spinning of the world. It is most easily seen with propulsive mass objects for long distances for example shells and missiles.

Q4. Does air resistance have a significant impact on projectile motion?

A: Air resistance indeed plays a large role in determining the direction and path of a projectile especially when the speed of the projectile is high or when the object in question has a large surface area.

Q5. How is projectile motion applied in sports?

A: Projectile motion, in its simplest form, is applied in most sports such as baseball, basketball, golf, and archery. By computing the trajectory path through launch angle and force, athletes give their best performance.