Applications of Rotational Motion: From Bicycle Wheels to Power Tools
What is Rotational Motion?
Consider the motion of a spinning top, a wheel or the motion of planets revolving around the sun. These are all examples of rotational motion! It is the rotation of an object with respect to a central axis which is also called the axis of rotation. While in linear motion objects have a straight line movement, rotational motion is unique as it involves movement in a circular form.
Examples of Rotational Motion in Everyday Life:
Rotational motion forms the basis of our world! It plays a part in something as basic as a doorknob’s handle or as complex as a car’s engine’s crankshaft.
Wheels: From automobiles, bicycles, to the wheels of clocks, rotational motion propels us forward or helps us tell time.
Machines: Rotational motion is responsible for powering motors, turbines and numerous other devices that we use in our day to day life.
Nature: We have day and night due to the rotation of Earth, and the rotation of stars and planets form our universe.
Fundamental Concepts
To understand rotational motion, we need to know some key concepts as follows:
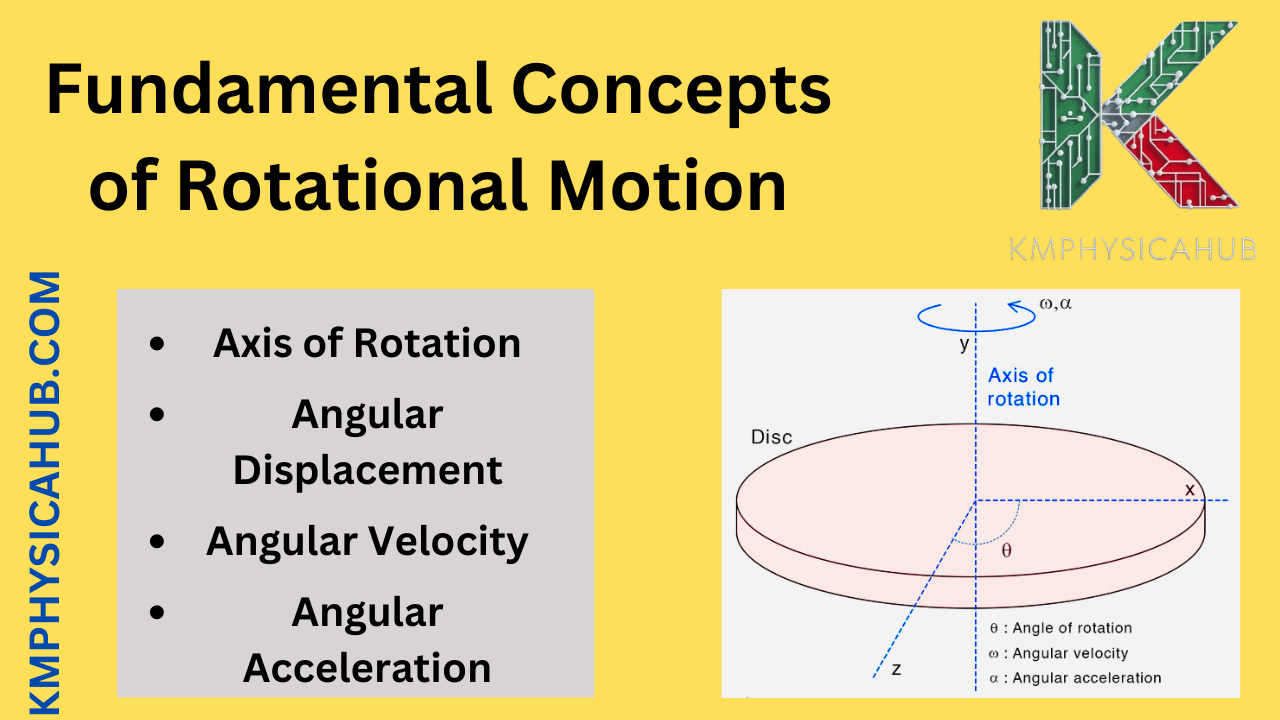
Axis of Rotation: A reference line along which any given object may revolve.
Angular Displacement: This defines how far through the circle an object has turned, like the angle traced by a spinning top.
Angular Velocity: This is used to determine the rate of revolution which is the speed at which an object is spinning such as a wheel.
Angular Acceleration: This measures how the angular velocity is being changed for instance the rate of deceleration of a spinning top.
Example:
Consider an arbitrary point on a rotating disc. If the disc is rotated around its axis then the point describes a circle. The amount of arc, represented by this point is the angular displacement measured in radians. Angular velocity is defined as the rate of change of angular displacement. It is like the rate at which the disc is spinning, and this is in radians per second.
Angular acceleration is the first derivative of angular velocity. It is like the rate of change of the angular velocity of the spinning disc, which is in terms of radians per second squared.
Relationship between Linear and Angular Quantities:
Let’s think about a point on a spinning disc again. This point has both linear and angular motion.
The linear velocity of the point is its speed along the circular path, while the angular velocity measures how fast the disc is rotating.
These two are related:
Linear velocity = radius x angular velocity
This simple equation connects the two types of motion.
Torque and Moment of Inertia:
Imagine pushing a door open. The force you apply causes the door to rotate. This force, applied at a distance from the hinge, is called torque. It’s the rotational equivalent of force in linear motion.
Now, imagine two doors, one made of wood and the other of steel. The steel door is harder to rotate because it has more inertia. This resistance to rotational motion is called moment of inertia. It’s like the rotational equivalent of mass in linear motion.
Types of Rotational Motion
Uniform Rotational Motion:
Think about a spinning top that is moving around in a circle with same speed. This is called uniform rotational motion. This means that the angular velocity of the object stays constant and there is no angular acceleration.
Non-Uniform Rotational Motion:
Think of a spinning top that is gradually decelerating. This is known as non-uniform rotational motion. Angular speed varies and there is angular acceleration with time.
Rotational Motion with Constant Angular Acceleration:
Think of a spinning top where the rate of spin is gradually increasing uniformly. This is referred to as rotational motion with constant angular acceleration. Angular acceleration is constant and therefore, the angular velocity increases with time in a straight line.
Conservation Laws in Rotational Motion
Conservation of Angular Momentum:
Just like linear momentum does not change if the external forces are zero, the angular momentum does not change if the external torque is zero. This means that the total of the angular momentum in a spinning body cannot vary and can only be constant even if mass describes the body in different ways.
Consider the example of figure skaters who twirl with their arms spread wide. When they pull their arms in, their moment of inertia reduces and angular velocity increases to maintain the angular momentum conserved.
Work and Energy in Rotational Motion:
Work can also be done in rotational motion like in linear motion. Work means the change in energy and in rotational kinematics, this energy in most cases refers to the rotational energy of an object. Overall energy of a system always remains conserved.
Work done by a torque: It is easier to explain this by bringing an example of how a torque is applied to a door. This torque will make the door to rotate and the work being done will be equal to the torque multiplied by the angular displacement.
Rotational kinetic energy: An object that rotates has kinetic energy given by the angular velocity of the object. This energy is directly proportional to the moment of inertia and the square of the angular velocity.
Applications in Everyday Life
-
Household Appliances:
Rotational motion is the basic working principle behind many common household appliances, making our lives easier and more comfortable.
Washing Machines: The working process of a washing machine is based on the use of a rotating drum and centrifugal force to compress water from the clothes.
Blenders: In a blender, blades continuously rotate in fast manner, effectively cutting or mixing the food.
Fans: The rotating blades in a fan make air to flow or in other words circulate and this leads to cooling and air circulation.
Drills: The spinning of the drill bit makes holes in different materials. These are commonly needed for construction.
-
Transportation:
Rotational motion is the backbone of our transportation systems.
Wheels: Through rotation of wheels, vehicles are made to move forward in the most efficient and with the smoothest motion possible.
Engines: The internal combustion engines use the movement of the pistons and crankshafts to convert the fuel energy into mechanical energy.
Propellers: Propellers in airplanes and ships work by rotating and create a force of thrust that pushes the aircraft or ship through the air/ water.
-
Sports:
Rotational motion plays a crucial role in many sports.
Baseball: The rotation in a baseball is able to give it movement in the air and lead to curves and breaking pitches.
Golf: Spin affects the golf ball in the air and can create variety of shots from the same position on the course at different distances.
Gymnastics: Rotations are the flips and twists that are often incorporated in the performance of gymnastic displays.
Figure Skating: Spins and other rotational movements are components of figure skating programs because they demonstrate elegance and dynamism.

Applications in Technology and Industry
-
Power Generation:
Turbines: In power plants, the steam is used to rotate blades of a steam turbine to produce electricity.
Hydroelectric Dams: Water flowing through dams turns turbines, therefore producing power from natural resources.
Wind Turbines: Electricity is created by the rotation of the blades and the force of wind power.
-
Manufacturing:
Rotational movement is quite significant in many manufacturing processes, where materials are formed and altered into the desired forms.
Machining: Turning and milling are groups of operations that employ cutting tools that rotate about an axis to cut metal and other materials into the desired form.
Drilling: Drilling machines involve use of cutting tools called drills which are in rotation as they cut and make holes on materials for different uses.
Grinding: Machines that operate with wheels which contain abrasive materials for shaping, smoothing, finishing surfaces are known as grinding machines.
-
Robotics:
Rotation plays a vital role in robot design and motion.
Robotic Arms: Joints of robotic arms, even if they are simply connected rods, enable the robot to move the limbs as needed.
Autonomous Vehicles: The use of wheels in self-driving cars allows them to move and steer on their own.
Applications in Science and Engineering
-
Astronomy:
The rotational motion plays an important role in the study of features and development of space objects.
Planetary Rotation: The spin of the planets affects climate, day-night cycle, and magnetic field.
Stellar Rotation: It has consequences on stellar age, brightness, and the distribution of elements within the stars.
Galactic Rotation: The rotation is a significant factor of galaxies, influencing both their formation and dynamics.
-
Physics:
Some aspects of rotational motion explain basic principles of physics.
Angular Momentum: The ability of a rotatory system to keep rotating, which is similar to the linear momentum of a moving body.
Torque: The directional equivalent of force that induces changes in angular momentum.
Conservation of Angular Momentum: In a closed system, which does not allow for transfer of angular momentum from outside, the total angular momentum remains conserved despite the changing form or modes of rotation of the object.
-
Engineering:
Rotational motion also finds practical use in a wide range of engineering fields.
Mechanical Engineering: Developing plans and testing mechanical structures such as machinery, engines, and other assemblies that incorporate rotating parts.
Aerospace Engineering: Explaining the rotational movement of aircrafts, space crafts and rockets.
Civil Engineering: Designing and analyzing structures that can support rotational forces, particularly in structures like bridges and buildings.
-
Future Applications
Emerging Technologies:
Rotational motion is expected to take on an even more prominent place in future technologies.
Nanotechnology: Rotational design and control of nanostructures for future material and devices.
Artificial Intelligence: Designing highly-mobile robots that can rotate efficiently with higher capability in tasks like surgery or exploration.
Energy Storage: Considering the possibility of using flywheels and their ability to store energy due to the rotational mass.
Challenges and Opportunities:
Following are the challenges that we face while harnessing rotational motion:
Efficiency: Enhancing the performance of rotational devices with reduced energy wastage and optimized efficiency.
Precision: Creation of enhanced methods for precise control of rotation movement, required by sophisticated applications.
Sustainability: Developing and implementing rotational systems that would be safe for the environment, and more importantly, sustainable.
Conclusion:
In conclusion, rotation is an integral concept in the existing universe, ranging from doorknob’s basic rotation to the swirls of galaxies. Through integration of angular displacement, velocity, acceleration, torque, and moment of inertia, the behavior of rotating matter can be described to foster the development of new technologies and inventions. Rotational motion is still a subject of intensive research in physics; innovative areas of interest include nano rotors, exotic rotation, and quantum rotation which open new horizons for future exploration, and improved understanding of the universe.
FAQs
Q1. What is the difference between linear and rotational motion?
A: Linear motion involves up and down movements while rotational motion is about the spinning around one selected point. Consider a car moving along a straight path (one-dimensional) compared to a spinning top (two-dimensional).
Q2. What are five everyday examples of rotational motion?
A:
- A bicycle wheel
- A washing machine drum
- A ceiling fan
- A spinning top
- A planet orbiting the sun
Q3. What are some applications of rotational motion in technology?
A:
- Power generation (turbines)
- Manufacturing (lathes, mills)
- Robotics (robotic arms)
- Transportation (car wheels, airplane propellers)
Q4. What is the relationship between rotational motion and gravity?
A: Rotation, which is an important category in the overall motion of objects in the universe is greatly influenced by gravity. Planets revolve around stars under gravitational forces, and the motion of stars and galaxies is determined by gravitational forces.
Q5. How does a figure skater spin faster when they pull their arms in?
A: This is a clear illustration of the principles of conservation of angular momentum. For instance, when the skaters pull their arms in, they reduce their moment of rotation.. Thus, to conserve angular momentum, their angular velocity (spin speed) has to increase.
