Recent Study Confirms: Hourglass Shape is Best for Hula Hooping

Mechanical systems that feature moving contact points, such as those found in rolling, sliding, and impact scenarios, are common in both engineering and everyday situations. The analysis of these systems becomes increasingly intricate when objects engage with the dynamic surfaces of moving structures, as illustrated by activities like hula hooping. 

A recent study conducted by researchers at New York University’s Applied Mathematics Laboratory investigates the underlying physics and mathematics that allow a hula hoop to appear to defy gravity, indicating that certain body types may be more advantageous for hula hooping. The research characterizes hula hooping as a form of mechanical levitation, driven by rolling points of contact and shaped by body morphology. 

The mathematicians involved in the study also pointed out potential applications for enhancing energy efficiency and improving robotic positioning. This study marks the first attempt to elucidate the physics and mathematics associated with hula hooping.

What is a Hula Hoop?

The hula hoop initially gained popularity as a toy for children. It consists of a circular plastic ring designed to be spun around the waist for extended periods until it eventually drops. Hula hoops are available in various colors, designs, and dimensions, with some models featuring lights. Additionally, there are hula hoops that incorporate ball bearings, beads, or bells, which produce sound when in motion.

Body Geometry and Movement

The physics of the Hula-Hoop has not been the subject of extensive research. Initial studies date back to 1960, coinciding with the toy’s rise as a modern craze, followed by another study in 1987. More recently, since 2008, a handful of papers have explored the topic again, driven by the Hula-Hoop’s resurgence in popularity as both a form of exercise and performance art. Most of this research has treated the problem as two-dimensional, typically modeling the hoop as a freely hinged extended mass or a ring moving along a circular path. 

However, these models fail to account for three-dimensional influences like gravity, specifically the mechanisms that allow the hoop to remain spinning and suspended for prolonged periods.

Hula-Hoop dynamics share many intricate elements with the physics of a spinning top (rotational motion), which involves a rotating rigid object influenced by “complex interactions between various degrees of freedom, as well as non-inertial reference frames and fictitious forces,” as the researchers described. 

Additionally, it incorporates unique challenges, such as the rolling point of contact on the surface of a body, driven by gyratory motions.

“We were specifically interested in what kinds of body motions and shapes could successfully hold the hoop up and what physical requirements and restrictions are involved,” says Leif Ristroph, an associate professor at New York University’s Courant Institute of Mathematical Sciences and the lead author of the study, published in the Proceedings of the National Academy of Sciences.

Just as a helicopter relies on precise blade movements and specific angles to remain in flight, a hula hoop requires particular conditions to sustain its graceful rotation around the body. Through robotic experiments and mathematical modeling, scientists identified two critical factors that determine whether the hoop will continue spinning or fall: the body must possess both “hips” (a sloped surface) and a distinct “waist” (an hourglass-like curve).

Robotic Experiments

To explore these dynamics, the research team developed small robotic hula hoopers at NYU’s Applied Mathematics Laboratory. They constructed these mechanical performers at one-tenth the size of a human, utilizing 3D-printed bodies in various forms, including cylinders, cones, and hyperboloids (hourglass shapes), to simulate different body types. 

These miniature dancers were activated by motors that mimicked human hip movements, while hoops measuring six inches in diameter were thrown around them. High-speed cameras recorded every wobble and spin. When a basic cylinder was tested, the hoop consistently fell. Similarly, a conical shape did not yield better results, though it produced more intriguing behavior. 

The hoop’s trajectory varied based on its release point; it either ascended the cone until it detached or descended until it fell off. However, when they evaluated a robot shaped like an hourglass, an extraordinary occurrence took place, the hoop located a stable position just beneath the narrowest part of the waist.

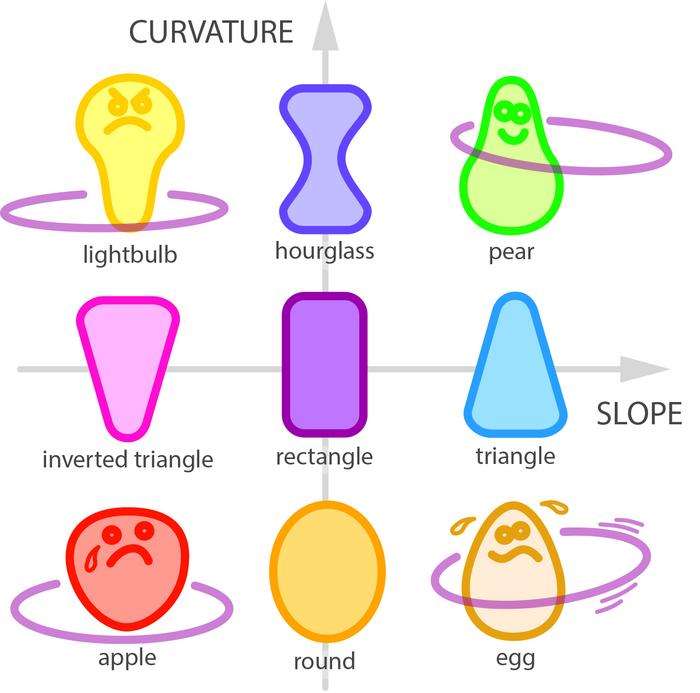
The researchers uncovered a surprising insight: the precise nature of gyration motion or the shape of the body’s cross-section, whether circular or elliptical, was not of great significance. The critical factor was the appropriate combination of slopes and curves. These results may clarify why hula hooping appears effortless for some individuals while proving challenging for others. 

“In all cases, good twirling motions of the hoop around the body could be set up without any special effort. People come in many different body types—some who have these slope and curvature traits in their hips and waist and some who don’t,” Ristroph observes. “Our results might explain why some people are natural hoopers and others seem to have to work extra hard.”

Some research findings support the intuitive understanding of hula hoop instructors accumulated over the years. For instance, it has been observed that beginners often find larger hoops more manageable—not because they are easier to see or grasp, but because their larger circumference facilitates the creation of more stable forces. It is noteworthy that the weight of the hoop is far less critical than its dimensions.

Spin Direction

An unexpected finding relates to the orientation of spin. Although many individuals picture the hoop rotating inward toward the body, effective hooping actually requires “direct outward twirling.” In this technique, the hoop remains in contact with the inner side of the body, while its center is oriented outward from the axis of rotation. The mathematical principles underlying hula hoop levitation may have implications that extend well beyond basic physics in playground settings.

“As we made progress on the research, we realized that the math and physics involved are very subtle, and the knowledge gained could be useful in inspiring engineering innovations, harvesting energy from vibrations, and improving robotic positioners and movers used in industrial processing and manufacturing,” says Ristroph.

Some Other Puzzles solved by Ristroph Team

Ristroph’s lab often tackles vibrant, intriguing problems inspired by everyday life. For example, in 2018, Ristroph and his team refined the formulation for creating the ideal bubble through experiments involving soapy thin films. In 2021, the Ristroph lab investigated the processes that lead to the formation of “stone forests,” which are prevalent in specific areas of China and Madagascar.

In 2021, his laboratory successfully constructed a functional Tesla valve, adhering to the original design of the inventor, and conducted measurements of water flow through the valve in both directions under varying pressure conditions. The results indicated that the water flowed approximately twice as slowly in the non-preferred direction. In 2022, Ristroph focused on the intricately complex aerodynamics that contribute to the performance of an effective paper airplane, particularly the requirements for achieving smooth gliding.

Last year, Ristroph’s laboratory solved the challenge posed by physicist Richard Feynman’s “reverse sprinkler” problem. They found that the reverse sprinkler rotates approximately 50 times more slowly than a conventional sprinkler, yet it functions based on similar principles. The key lies within the sprinkler itself, where jets cause it to behave like an inverted rocket. Instead of the internal jets colliding directly, the water moves around the curves in the sprinkler arms and is propelled outward by centrifugal force, resulting in asymmetric flow.

The paper’s other authors were Olivia Pomerenk, an NYU doctoral student, and Xintong Zhu, an NYU undergraduate at the time of the study.

The work was supported by a grant from the National Science Foundation.

Conclusion

In conclusion, the study not only demystifies the art of hula hooping but also emphasizes the intricate relationship between body geometry and physical dynamics, with potential implications that stretch far beyond the playground.