Entropy: Understanding Complexity, Disorder and Arrow of Time

Definition and Fundamentals

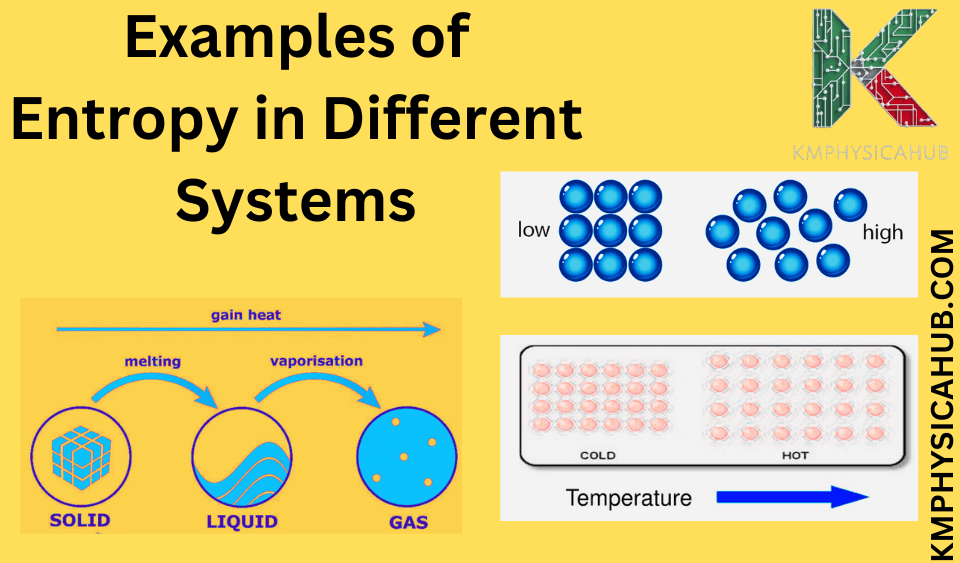
Suppose we have a box in which there are some atoms and molecules of the gas. All the molecules move around chaotically and collide with each other producing melodious motion of molecules. This disorder is what we refer to as entropy, a state of randomness and confusion. In more basic term, entropy is the amount of chaos in a given system. Every additional mode of arrangement adds to the entropy or the randomness of the system.

But entropy is not only the randomness or disorder; entropy is one of the most essential concepts of thermodynamics that dictates the distribution of energy and the arrow of time. It explains why a hot cup of coffee cools down and why a broken egg does not come back together on its own, and even why the universe appears to be gradually running down.

Entropy in Classical Mechanics:

Classical mechanics, which is a set of laws, deals with the description and prediction of the motion of bodies influenced by forces. But it only provides a restricted view of entropy. Classical mechanics does not define it specifically in a clear-cut manner although some grey area concepts may be mentioned. Though we can describe it as the extent that a system takes in phase space, or a space representing all possible configuration of a system in terms of position and momentum of the system, this doesn’t fully explain entropy as a measure of chaos.

The Role of Statistical Mechanics:

In comes statistical mechanics, the branch of physics in which we explore the atomic and molecular realm. It also fills the gap between the large-scale motion described by Newton’s mechanics and the small-scale motion at the atomic and molecular levels. Statistical mechanics further helps in conceptualizing entropy through the relationship between entropy of a system and the probability distribution of microstate of that system.

Suppose we have a system with a large number of particles. Every particle can be in different states and therefore there are countless possibilities, or microstates, for arranging the individual particles.

Entropy in Hamiltonian Mechanics

• The Liouville’s Theorem:

Hamiltonian mechanics offer a well-formalized set of equations which can be used for the analysis of various conservative systems. Liouville’s theorem, which is one of the key postulates of Hamiltonian mechanics, affirms that the phase volume of a system does not change with time. 

Think of a swarm of particles moving in phase space. As they are moving, the place they occupy as well as their velocity also change, however the total volume they occupy does not alter. This conservation of phase space volume is an immediate result of the deterministic dynamics governed by Hamiltonian mechanics.

• The Boltzmann Equation:

The Boltzmann equation which is the fundamental equation in statistical mechanics relates entropy to the probability distribution of micro states. This tells us that the entropy of a system according to Boltzmann is equal to the average logarithm of the probability of each microstate.

Suppose that the given system has a very large number of microstate possibilities. The probability of different microstates is higher or lower depending on the energies of the system and other considerations. The Boltzmann equation indicates that the entropy of the system is greater if the probability density of the microstates is more even, that is, if all the microstates are equiprobable.

• Ergodicity and Mixing:

In Hamiltonian systems, ergodicity and mixing are crucial concepts related to entropy. An ergodic system is one that, over long periods, explores all possible microstates in phase space. A mixing system is one where initially distinct regions of phase space become increasingly intermingled over time.

Ergodicity and mixing are essential for increase of disorder in Hamiltonian systems. If a system is ergodic and mixing, it will eventually explore all possible microstates, leading to a more uniform probability distribution and higher entropy.

• Second Law of Thermodynamics:

The second law of thermodynamics is one of the most accepted laws in nature, describing that the entropy of a closed system will always tend to increase over time. It is believed that the second law of thermodynamics as defined in Hamiltonian mechanics can be derived from ergodicity and mixing.

Imagine a closed system with a non-uniform probability distribution of microstates. As the system evolves according to the Hamiltonian equations of motion, it will explore different regions of phase space.  If the system is ergodic and mixing, it will eventually explore all possible microstates, leading to a more uniform probability distribution and higher entropy. This increase in disorder is a predicted result of the second law of thermodynamics for Hamiltonian mechanics.

Entropy in Dissipative Systems

• Role of Friction and Dissipation:

Although the Hamiltonian approach describes ideal systems with conservative forces, real-world systems act with dissipation forces, such as friction, viscosity and drag forces. These force work in a manner that reduces the total amount of energy in the system.

Consider a simple example: a moving pendulum in the air. The pendulum bob will eventually settle down due to air resistance which limits its further kinetic energy. This energy dissipation makes the process irreversible and this means that the energy contained in the system cannot just revert back on its own.

• Entropy Production in Dissipative Systems:

It is important to note that dissipative forces remove energy from the system and also create entropy. When energy is lost, the system migrates to a state that contains a greater proportion of microstates and, therefore, more disorder.

For example, the pendulum would lose energy due to air resistance and would eventually come to thermal equilibrium with its environment. This thermalization process implies an enhancement of the entropy of the pendulum and also of the surrounding air.

• Examples of Dissipative Systems:

Energy dissipation occurs in every physical process of the Universe and is pivotal for our understanding of the world. Here are some examples of mechanical systems with dissipation:

Damped Oscillators: 

An object such as a mass attached to a spring due to a damping force like friction will eventually lose its energy and come to rest. Entropy rises as heat energy is transformed to other forms of energy or is dissipated into the environment.

Fluid Flow:

 Viscous forces are the forces that occur in fluids in motion and these forces bring about dissipation of energy. This dissipation is the source of heat production which in turn causes entropy to rise.

Heat Conduction: 

Whenever there is a physical contact between a hot object and a cold object, heat energy tends to transfer from the hot object to the cold object. Heat transfer is a dissipative process that involves a general rise in disorder or randomness in the system under consideration.

• Connection to Thermodynamics:

Dissipative structures generate randomness and hence are directly associated with the second law of thermodynamics. The second law states that the entropy of a closed system can only increase or remain the same. This increase of disorder in dissipative systems is obligatory resulting from energy dissipation.

Consider an isolated system in which there is a damped oscillator. With the loss of energy by the oscillator due to friction, the entropy of the oscillator increases. As the heat energy released through friction is conducted to the environment, this results in an increase in the disorder of the surrounding. The total entropy of the entire system comprising the oscillator and the environment either stays constant or increases.

Entropy in Chaotic Systems

• Defining Chaos:

Chaos is of great interest in dynamical systems; it is the effect where very slight changes in the initial conditions produce significantly different future states. This sensitivity to initial conditions is known as the “butterfly effect. ”

Consider two swings completely similar to each other but set into oscillation from slightly different phases. Over time, their swings will diverge significantly, even though they are governed by the same physical laws. This divergence is a hallmark of chaos.

• Lyapunov Exponents:

Lyapunov exponents are another mathematical measure of chaos that estimate how fast distances between neighboring trajectories grow in the course of dynamics. When Lyapunov coefficients are positive, it suggests that the system is chaotic and they are negative for a stable system.

The rate of entropy production in system evolution is directly connected with the use of the Lyapunov exponents. Thus, the disorder of the system increases more when the Lyapunov exponents are larger.

• The Butterfly Effect:

A perfect example of chaos, butterfly effect shows how entropy in the system increases exponentially. To briefly explain the butterfly effect, it is an academic concept stating that a slight variation in the starting conditions, such as the flapping of a butterfly’s wings, can result in massive consequences in the overall system.

This exponential growth of entropy is due to the fact that the system has a sensitive dependence on the initial conditions. Small differences at the beginning are multiplied over and over again until the overall disorder or, in other words entropic value of the system becomes very large.

• Implications for Predictability:

The fact of the exponential growth of entropy in a chaotic system has terrific consequences for the predictability. Due to the ideal sensitivity to initial conditions, it is extremely hard to predict long-term behavior of chaotic systems with absolute certainty. If there exists the slightest doubt in the accuracy of the quantification of the initial conditions, then the extent of the error will increase exponentially, making long-term forecasts impossible.

Imagine trying to predict the weather. The model of the atmosphere is characterized as a chaotic system in which there are millions of factors that affect its functioning. If there was a small mistake in the first facts about the weather, such as the wind speed, after several days, the forecast may be completely different.

This is not due to that we do not know enough, or that the models for these chaotic systems are imperfect or incorrect. This is actually a direct outflow of the fact that any goals set for these systems are inherently unstructured and unpredictable.

Applications and Implications

• Entropy and Statistical Physics:

Entropy occupies a central position in statistical physics as a way of describing equilibrium and non-equilibrium systems.

Equilibrium:

In equilibrium, it is said that the entropy is maximum and represents all possible microstates that any system can take given its energy and other conditions. The entropy is very useful in determining characteristics of matter at equilibrium, for instance, distribution of particles in a gas or phase of liquids and solids.

Non-equilibrium: 

In nonequilibrium systems, the entropy is still rising as the systems belong to the state which is more random. It is important to consider entropy generation in non-equilibrium systems to study heat transport, chemical reactions, or biological processes.

• Entropy and Information Theory:

It is directly related to information theory, in which it is used as a measure of uncertainty or randomness of a message or data.

Suppose you have a message which is encrypted in a certain set of symbols. The higher the number of symbols within the message, and also the more balanced these symbols are in relation to the message, the higher the entropy in the message. This means the message is more uncertain, making it harder to predict.  

Conversely, a message with low disorder is highly predictable, as the symbols are less varied and more concentrated.

• Entropy and Biological Systems:

In the context of biological evolution and origins of life, it has metaphysical significance for the behavior of biological systems.

Evolution: 

Evolutionary processes are fundamentally associated with the entropy of the universe. As the amount of disorder in the universe increases, biological systems’ organization and complexity can only be sustained and renewed constantly. This fight against disorder is in fact the essence of evolution.

Origin of Life: 

The origin of life from a lifeless material is a great transition which results in a decrease in the entropy. However, this appears to violate the second law which is only possible because living organisms as open systems consistently exchange energy and mass with their surroundings. While there is a decrease in its amount within the organism, it is overwhelmingly counter-balanced by an increase in disorder with the surroundings, which still puts the total entropy in the universe on the right side of the law.

• Entropy and Cosmology:

It is an essential concept in cosmological studies, especially with reference to the Big Bang and the direction of time.

Big Bang: 

The Big Bang theory puts forward a proposition that the universe had a beginning in a hot, dense, low disorder state. As the universe expanded and cooled the entropy becomes high and finally galaxies, stars and planetary systems were generated. This increase in disorder is an inherent feature of cosmological processes in the evolution of the universe.

Arrow of Time: 

The second law of thermodynamics is said to hold the key to the flow of time from the past through the present to the future, which is known as the arrow of time. The element of increase in disorder of the universe is considered as the major driving force behind this arrow of time. Nevertheless, it is still not clear how entropy is connected to the arrow of time, as it remains an object of the discussion among physicists.

Conclusion:

Entropy was regarded only as a measure of chaos, but it turned out to be one of the most significant and important concepts in physics. It controls the direction of energy, determines time’s course, and is in the center of the universe. Thus, it remains to be an invaluable tool as we progress in the understanding of the workings of the universe. The deeper we get in this disorder, the more we get the point that entropy is not only an idea, but a fact of existence.

This exploration of disorder and randomness has taken us from the mechanical world of the early twentieth century to the statistical world of today.

FAQs

Q1. How does entropy relate to heat?

A: Heat is a type of energy transfer associated with thermal difference. Heat always flows from an object of higher temperature to an object of lower temperature and therefore the entropy of the system increases.

Q2. Write three examples of entropy in everyday life?

A: 

1. Melting ice
2. Mixing sugar in water
3. Burning wood

Q3. Can entropy ever decrease?

A: Yes, it can be reduced in a local system. However, this is only possible at the expense of a greater disorder in the surroundings. As a result, the total entropy of the universe is still increased.

Q4.  Is there a “heat death” of the universe?

A: The heat death scenario paints a bleak picture: as the universe grows, so does disorder and it reaches the maximum entropy at the end of time. Heat is spread uniformly and reaches thermal equilibrium, a condition in which no more work can be performed. It would make the universe a cold, dark and an empty place.

Q5. What are some of the open questions regarding entropy?

A: 

1. Its role in quantum systems
2. The exact connection between entropy and the arrow of time
3. The future implications for exploring universe