From Space Exploration to Science Fiction, Applications of Escape Velocity
Defining Escape Velocity
Escape velocity is the velocity required to permit an object to travel away from the surface of any planet or moon and become incorporated into space. It is the speed when the kinetic energy is equal to the gravitational potential energy, and the object can escape the earth’s gravitational field or pull of the celestial body and move further away into the infinite region.
Illustration through Example:
Now picture as though you are tossing a ball upwards directly towards the sky. It will ascend, accelerates, and come back to Earth because of gravity. But if you chuck it hard enough, and it is not weighed down by anything, it will go on rising and rising until it floats away from the pull of the Earth. This minimum speed that is needed to escape is referred to as escape velocity.
Importance:
The escape velocity is essential for knowing the behaviors of the universe and how we the mankind can traverse it. It defines the possibility of putting spaceships and other satellites into orbit, the characteristics of celestial bodies, and the structure of galaxies and their development. The escape velocity therefore is a measure of the minimum speed one has to achieve to be able to leave the gravitational influence of a certain planet, star, or any other massive object and penetrate the cosmos.
Historical Context
Early Understanding:
The theory of escape velocity originated with Isaac Newton in the 17th century through the use of his laws of motion and universal gravitation. Nevertheless, concepts of escape velocity did not come into the category of real applications until rocket technology emerged in the twentieth century.
Rocketry and Space Travel:
Innovators such as Robert H. Goddard and Konstantin Tsiolkovsky understood and studied escape velocity for space exploration. Their efforts were the building blocks of today’s rocket science and birth of a space vehicle, capable of attaining escape velocity and go beyond our atmosphere.
Concepts Involved in Escape Velocity
Gravity: The force due to which objects with mass attract each other; the greater the attraction of a celestial body, the greater the speed needed to break its effect.
Kinetic Energy: Energy associated with an object in transfer or movement from one place to another. For an object to escape the pull of gravity, it requires enough energy to overcome the gravity field energy.
Potential Energy: The energy that an object has in any given field because of its position relative to a massive body. The height of the object determines its capacity as a potential energy holding body.
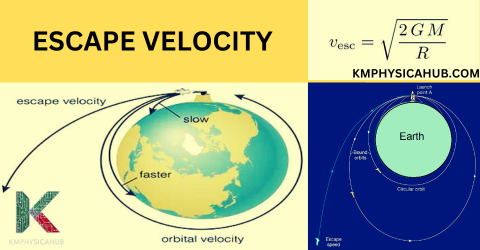
Mathematical Derivation
Setting Up the Equation:
Suppose a body of mass m is fired straight up from a planet of mass M and radius R. The object’s initial kinetic energy (KE) is:
KE = (1/2) * m * v^2
where the initial velocity of the object is referred to as v.
The object’s initial potential energy (PE) due to the planet’s gravitational field is:
PE = -G * M * m / R
where G is the gravitational constant.
Applying Conservation of Energy:
While moving above, the distance from the planet increases. It results in a decrease in kinetic energy and an increase in potential energy. In escape velocity, the kinetic energy of the object which is being sent off is equivalent to the potential energy:
KE = PE
(1/2) * m * v^2 = -G * M * m / R
Solving for Escape Velocity:
Solving the above equation for v (escape velocity), we get:
v = √(2 * G * M / R)
The above equation reveals that escape velocity is proportional to the square root of mass (M) of the celestial body and inversely proportional to the square root of its Radius (R).
Applications in Space Exploration
Launching Spacecraft and Satellites:
The velocity needs to be achieved by a spacecraft or a satellite to place it in orbit around the earth is called orbital velocity. This velocity is slightly below the escape velocity and as a result the satellite stays in the orbit and does not escape earth’s gravitational force. But getting the spacecraft to travel to another celestial body such as the Moon or Mars requires a higher velocity known as escape velocity.
Achieving Escape Velocity:
Thus, rockets and spacecraft, in order to gain escape velocity, need to have engines capable of creating enough thrust. The quantity of fuel also has a direct correlation with the escape velocity, which further asserts the need for good designs for the engines as well as optimized fuel usage in space missions.
Interplanetary Missions:
When it comes to these missions, spacecrafts are required not only to escape the gravity of Earth, but to increase their velocity further to get to the target planets. In this context, escape velocity calculations play a very important role in estimating the amount of fuel and power a spacecraft will require for such a mission, to possess enough energy to get out of both the Earth’s and the target planet’s gravitational fields.

Applications in Astronomy
Understanding Black Holes:
Black holes are regions in space that confine gravitational pull so heavily that nothing, including light, can emerge from the center. This is because the escape velocity is greater than the speed of light at the surface of event horizon and therefore leaving a region where nothing can emerge. An appreciation of escape velocity is useful when making sense of how powerful black holes are and how they transform spacetime.
Studying Neutron Stars:
Neutron stars are very closely packed collapsed stars which possesses very strong gravitation force. Escape velocities they possess are remarkably high and range from 100,000 km/s and above. Science can learn about the structure of neutron stars and the physics of ultra-strong gravity in the open by examining patterns in their escape velocities.
Galactic Dynamics:
Another aspect of galaxy motion is established by the concept of escape velocity. The concept of escape velocity is crucial for finding the minimum velocity necessary for objects like stars or gas clouds to be set free from a galaxy’s gravitational influence. It affects the motion of material within galaxies and their development over time.
Everyday Life Applications
Fluid Dynamics: The rate that a fluid can escape from one cavity to another as in the examples of water escaping from a punctured bottle, is normally determined by the pressure difference between the outside and the inside of the container. Larger pressure differences mean larger escape velocities for the celestial bodies.
Particle Physics: In particle physics, the ability of particles to escape from a potential well such as nucleus involves a measure called escape velocity which depends on the forces that bind the particles together. Objects with more kinetic energy have possibilities to leave the potential well, whereas the objects with lesser kinetic energy are trapped within this well.
Sound Waves: The speed of sound in a given medium can also be regarded as the escape velocity of waves with regard to the given medium, be it air or water. Sound waves must move through the medium faster than the escape velocity to propagate through it.
Escape Velocity in Science Fiction
It has been often used in science fiction novels, films and video games, being a very popular tool to create suspense or as a plot element. In star stories people often hear about the concept of velocity that is required to get away from the planet’s attraction or the view of getting away from one solar system to another. For instance, in the popular movie ‘Star Wars,’ the protagonists in the spaceship known as the Millennium Falcon have to attain a certain velocity to get off the Death Star.
Escape velocity has also been utilized in science fictions to portray a climactic scene that involves astronauts trying to escape from a certain planet or even individuals who have been trapped by black hole. It has become an easily recognizable and a leading concept in the global society and entertainment industry, helping to create a realistic and dangerous undertone in stories based on space travels.
Limits of Escape Velocity
While escape velocity is a fundamental concept in astrophysics, it also has its limitations:
Relativistic Effects: Newtonian physics is imprecise at velocities near the speed of light, and therefore, one cannot use escape velocity equations in this particular range of velocities. General relativity has to be taken into account to describe how objects respond to such immense fields.
Alternative Propulsion Systems: Other theoretical solutions such as the warp drives and worm holes in case they are given the green light can make it possible to travel at light speed and therefore escape velocity would not be an issue at all.
Unknown Physics: The general understanding of gravity and spacetime is not yet fully developed and thus there may be other unexplored physical processes or forces that may impact the escape velocity or other methods of negating the effects of gravity.
Conclusion:
Escape velocity in physics is a principle that is of much importance in the study of the laws governing the universe and our interactions with them. It is a threshold speed that determines whether an object will be locked to a celestial body or simply be thrown out into the space. Explaining how the escape velocity is derived from the fundamental physics, shows that it depends on the mass and the radius of the celestial body. The real-life applications are also shown through rocket launches, satellites, and interplanetary travels. Studying the principle of escape velocity is helpful in analyzing the complexities of space objects and the difficulties associated with them.
People Also Ask
Q1. What is escape velocity?
A: The least velocity required to make an object leave off the surface of a celestial body and finally move out into interplanetary space.
Q2. What factors affect escape velocity?
A:
Mass of the celestial body
Distance from the center of the body.
Q3. What is the role of escape velocity in space exploration?
A: It defines the speeds for placing spacecrafts and satellites into space and therefore influences the use of fuel and the possibility of the mission.
Q4. Does escape velocity change for different celestial bodies?
A: Yes, it depends on the mass and radius of the body or object under consideration.
Q5. What happens if an object doesn’t reach escape velocity?
A: It shall either crash on the celestial body or orbit around it with a specific distance.
