Moment of Inertia: Concepts, Formulas and Interesting Applications

Inertia:

Think about when you are attempting to slide a large box on the floor. It requires some work to set it into motion. That is the common principle known as inertia; which is the ability of an object to resist the change in its motion. Inertia depends on the mass of the object if the box is heavier in fact when a man tries to push the box, it will be difficult which means that the percentage of inertia on the box is high.

Moment of Inertia:

Now, imagine that you are to spin that very box. You would quickly observe that how easy or hard it is to rotate depends not only with the mass, but where that mass is situated compared to the axis of rotation. The moment of inertia comes into play at this point. It is very analogous to what can be referred to as the “rotational inertia” of an object.

Understanding Moment of Inertia

Definition and Mathematical Representation: 

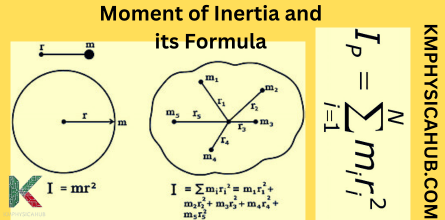
Moment of inertia (I) is the sum of the product of mass of each particle ‘m’ in the body and square of the distance r of the particle from the axis of rotation.

    I = Σmr²

Importance of moment of inertia:

Moment of inertia is important to determine the rotation of an object and the forces that act on it. It is widely involved in such areas as engineering (creation concerning flywheels, turbines, etc. ), sports (for instance, figure skating spins, a baseball bat movement), and in understanding of motion of planets and galaxies.

Factors Affecting Moment of Inertia:

Mass (m):

Moment of inertia increases with the mass of the object because more significant amounts of mass creates larger distances from the center of rotation. People have just found it more difficult to spin objects that are larger in mass around.

Mass Distribution (r):

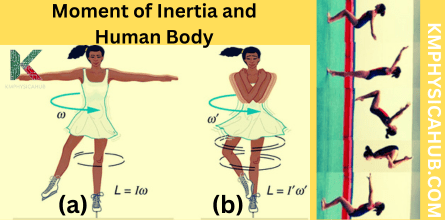
If the mass is accumulated at the middle of the circle or along the axis of rotation, the moment of inertia is lesser. And if the mass is displaced away from the axis, then the moment of inertia will be higher. Likely to the situation when a skater spins faster after pulling his arms in – skaters can spin as they have reduced their moment of inertia.

Radius of Gyration (k):

This is a useful, yet simple, conceptual framework. Suppose the whole mass of an object can be transported and condensed to a point at a particular distance from the axis of rotation. The radius of gyration (k) is that distance. It is used to indicate the procedure of distribution of mass for rotatory movement of an object.

Calculating Moment of Inertia

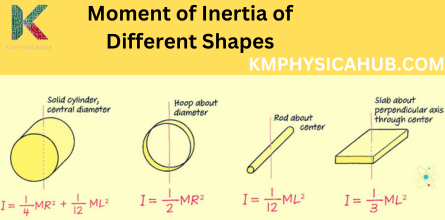
• Simple Shapes:

Point Mass: The simplest case! I = mr² (where ‘r’ is the distance from the axis).

Rod (about its center): I = (1/12)ML² (where ‘L’ is the length of the rod).

Disc (about its central axis): I = (1/2)MR² (where ‘R’ is the radius of the disc).

• Complex Shapes: 

Parallel Axis Theorem:

This theorem is applied where we have to find the moment of inertia of a rigid body about an axis which is parallel to an axis passing through the center of gravity, so we require the moment of inertia of the body about the center of gravity.

Perpendicular Axis Theorem:

This theorem is for the situations where objects exist in two dimensions (they are flat). This theorem assists us in knowing the moment of inertia about an axis perpendicular to the plane of the object, if we are given the moments of inertia about two perpendicular axes within the plane.

Everyday Objects and Moment of Inertia:

Rotating Objects:

Open your eyes and you will find that all around you there are many places where the moment of inertia is defining how a rotating object will behave. A spinning top, for example will not easily change its direction of spin because of its moment of inertia. Unlike with cars, bikes have a larger wheel diameter and a larger mass in the outer circumference of each wheel, making the moment of inertia more in cycles, thus offering smoother rides. From the blades of a ceiling fan to the blades of a commercial airplane, it is all about capturing, controlling and directing moment of inertia in the simplest terms-so as to get optimum flow.

Stability and Balance:

The moment of inertia also has significant impacts on bodily functionality in terms of maintaining an upright posture and manner of walking. As we move our legs in walking, we hold our arms to swing them so as to add a moment of counter inertia, thus improving balance. Tightrope walkers commonly use long sticks because they add to the center of mass and prevent easy falling off. Just holding an item whose weight is considerably greater than that of our arms, alters our body’s balance, or center of mass, and moment of inertia.

Applications of Moment of Inertia

• Transportation:

Moment of inertia is a fundamental consideration in vehicle design:

Cars: The moment of inertia of a car determines how the car responds and steers while in motion. A small moment of inertia, it is possible to achieve by placing more weight nearer to the center of the vehicle which provide better turn facility.

Airplanes: Jet engines have enormous rotating blades which have a large moment of inertia, and proper consideration of this aspect must be given during design and operation. The same could be said for the distribution of weight in an aircraft as distribution of weight influences an aircraft’s stability and maneuverability.

Trains: The velocity of the high-speed trains is chosen to have calculated moments of inertia in order not to derail and to achieve high comfort.

• Machinery and Equipment:

It goes without saying that vast number of industrial applications employs the rotation of its components and therefore the moment of inertia is always amongst the crucial design parameters.

Gears: Machinery which may require different moments of inertia are designed with gears to allow control of speed and torque in their operation so that power transmission may be smooth.

Turbines: Turbine blades, which are used in power plants and jet engines are made up of large and massive rotating units that are designed to have very high moment of inertia and hence are very stressed.

Motors: Electric motors require rotating parts with fixed moments of inertia to produce the set speeds and torque levels.

• Robotics:

In robotics, moment of inertia most importantly plays a crucial role in the ability and stability of a robot, and its precision.

Movement and Manipulation: The robotic arms and manipulators are constructed with very specified moment of inertia for each joint so as to facilitate the control of movements and shapes on the objects.

Balance and Locomotion: There are walking robots and drones that have complex control systems to continuously change the moment of inertia to facilitate movement and balance.

• Engineering Design:

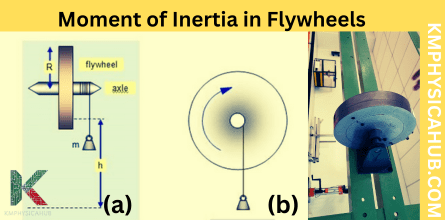
Flywheels: These mechanical wonders use their high moment of inertia in order to store rotational energy. They are used to reduce fluctuations in rotational speed and have uses in various applications including engines, power plants, and even regenerative braking.

Crankshafts: Core to internal combustion engines, crankshafts transform the up-and-down motion of pistons into circular movement. Their layout pays much attention to the mass specific momentum so as to deliver power with minimal vibrations.

• Sports and Recreation:

Figure Skating: The positioning of a figure skater in their spin is solely an outcome of their control of moment of inertia. To clarify, when they flex their arms and legs, they reduce their moment of inertia, and as a result the spin speeds up significantly.

Gymnastics: When a gymnast performs a rotation on the uneven bars or during the flips, twists during the floor exercise, the concept of moment of inertia becomes vital when trying to display control over the rotations in the air.

Moment of Inertia and the Human Body

• Movement and Posture:

The human body is a complex system of bones interacting with each other, and moment of inertia is a factor in its operation:

Walking and Running: Our legs are like pendulum while walking or running and their moment of inertia determines our cadence, stride length, and energy demand.

Jumping: When jumping, we automatically and unconsciously, bend our knees which leads to decrease of our moment of inertia and thus we create a way of exhibiting more force in the upwards direction.

• Injury Prevention:

Knowledge of moment of inertia is vital in order to avoid some injuries especially in exercises and games that involve rotation:

Warm-up and Stretching: Flexibility exercises help to enable muscles and joints to respond to changes in the rate of inertia throughout the course of activity.

Proper Technique: In the movements of sports and exercises, there are also principles of how to apply and use the moment of inertia in avoiding force on the joints and increasing the force exerted by muscles.

Conclusion:

One of the principal concepts of dynamics of a body is the moment of inertia which quantitatively describes the body’s ability to counteract the external interferences to its rotation. This means that it does not only depend on how massive the object is but also the way the mass is distributed with respect to the axis of rotation.

In future with technology growing and our systems getting more complex than today the concept of moment of inertia will assume a big role. Scientists and engineers go on discovering new materials and more effective ways of designing to implement the moment of inertia in different fields as desired.

People Also Ask

Q1. What is moment of inertia?

A: Moment of inertia can be regarded as rotational equivalent of mass; an object with a greater mass is harder to move, and an item with a higher moment of inertia is also harder to spin or to prevent from spinning.

Q2. Which factors affect moment of inertia?

A: The two important factors are mass of an object and its distribution along the axis. With the increase in the distance of mass from the axis of rotation, moment of inertia also increases.

Q3. What is the relation between angular momentum and moment of inertia?

A: When moment of inertia and angular velocity are multiplied, we get angular momentum. This relation helps in understanding the behavior of an object when its rotation changes.

Q4. Give three everyday examples of moment of inertia?

•  Tightrope walker’s pole: It increases their moment of inertia thus balancing can be easily made.
• Figure skater’s spin: Pulling in their arms reduces moment of inertia, increasing spin speed.
• Bicycle wheels: Mass concentrated at the rim gives them a higher moment of inertia for smoother riding.