Applications of Simple Harmonic Motion: From Pendulums to Spring-Mass Systems

Simple Harmonic Motion (SHM)

Consider a body oscillating up and down such as a vibrating spring or simple pendulum. These are some common examples of Simple Harmonic Motion (SHM). This is a particular kind of oscillatory motion characterized by the fact that the force that acts towards equilibrium is directly proportional to the displacement measured from the equilibrium position and always in the opposite direction.

It is like a ball tied to a spring. If you pull the ball away from the position where it’s resting, it’s like the spring is trying to slam it in the middle. The force exerted to pull it back is proportional to the amount by which it has been stretched or compressed.

Examples of SHM in Everyday Life:

Pendulums: From clocks and swings to the gentle swaying of trees in the wind.

Springs: Suspension systems of cars, toys like bouncy balls or even strings of a musical instrument.

Sound Waves: The movement of air molecules creating sound waves is an example of SHM.

Light Waves: Light is itself a wave, and the patterns of oscillations follow the SHM model.

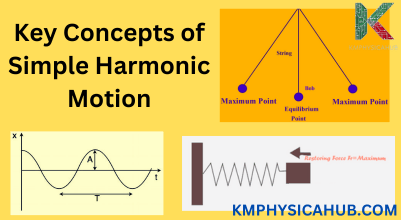
Key Concepts of SHM

• Displacement, Amplitude, Period, Frequency:

Displacement: 

The motion involves something like a ball tied to a spring, with the ball oscillating vertically. Displacement is how much it is moved from the state of equilibrium (this is the state where there is no extension or compression of the spring). It is actually a vector quantity because it has magnitude (how far) and direction (up and down).

Amplitude: 

The amplitude is the maximum amount of displacement possible in the oscillation from the equilibrium position. It is similar to the ‘size of oscillation.’ Just as a pendulum swings back and forth. The amplitude is the maximum extent of the angle by which it moves on either side of the vertical position.

Period: 

The period is the time for one complete cycle of the motion. It is the time that is taken in moving from one high point to the next high point or from one low point to the next low point. Consider a clock’s pendulum. The period is the time it takes to go back and forth once.

Frequency: 

The frequency in turn is defined as the number of times the cycle is repeated in one second. It’s the inverse of the period: f = 1/T, Higher frequency indicates more oscillations or vibrations per second, like a rapidly beating humming bird’s wings.

Relationship between Period and Frequency: 

It is clear that there is an inverse relationship between Period and Frequency. A long period of time will produce a low frequency rate while a short period of time will produce a high frequency rate. Think about a pendulum that swings back and forth – it does not move from one position to another very often, so the frequency is low.

• Restoring Force and Equilibrium Position:

Definition of Restoring Force: 

The restoring force is force that is always in opposition to the motion of the object and brings the object back to its position of rest or equilibrium. It is the force by which the oscillatory motion is generated. Think of the spring pulling the ball back towards its rest position.

Relationship between Restoring Force and Displacement: 

In SHM the restoring force is directly proportional to the displacement from the mean position or average position. This means that the force that tries to bring the object back to its equilibrium state increases as the distance from the equilibrium position increases. This is described by a principle known as Hooke’s Law, which we’ll discuss more fully later.

Equilibrium Position: 

The equilibrium position is the position where the net force acting on the object is equal to zero. This is the state where the object would be found if it is not interfered by other forces. In the spring-ball example, the equilibrium point is the point where the spring is not compressed and the ball is not moving at all.

• Hooke’s Law and its Relation to SHM

Statement of Hooke’s Law: 

According to Hooke, the restoring force of a spring is directly proportional to the amount of displacement from the equilibrium state.

Mathematically, this is expressed as: 

F = -kx

where:

• F = The restoring force
• k = The spring constant (a measure of the spring’s stiffness)
• x = The displacement from equilibrium

Mathematical Representation of Hooke’s Law: 

The negative sign used in Hooke’s Law means that the force applied is always in the opposite direction to the displacement. When you elongate the spring in the right direction, the force that is exerted over it tends to pull it to the left and so does the same for the left direction.

How Hooke’s Law applies to SHM: 

Hooke’s Law is the basis of analysis in SHM. Since the restoring force is directly proportional to the displacement, the object moves to and fro in a sinusoidal manner.

• Simple Harmonic Oscillator

Definition of a Simple Harmonic Oscillator: 

Simple harmonic oscillator is a system that is involved in SHM. It is a system where the restoring force depends on the displacement, and the movement describes the form of a sine wave.

Examples:

• Mass-Spring System: 

The simplest example of a physical system displaying simple harmonic motion is a mass attached to a spring. The restoring force is provided by springs while mass moves to and fro.

• Simple Pendulum (for small angles): 

Another physical system, which demonstrates features of SHM is a simple pendulum that is made of a mass attached to the string. The restoring force is due to gravity, which tends to bring the pendulum back to the central vertically suspended position.

Mathematical Description of SHM

Equations of Motion (Displacement, Velocity, Acceleration):

Mathematically, SHM can be represented in terms of sinusoidal functions. Following are the equations for displacement, velocity, and acceleration:

Displacement (x): 

x(t) = A * sin(ωt + φ)

Velocity (v):

v(t) = Aω * cos(ωt + φ)

Acceleration (a):

a(t) = -Aω² * sin(ωt + φ)

Where:

A is the amplitude

ω is the angular frequency (ω = 2πf = 2π/T)

φ is the phase constant, which determines the initial position of the object

Sinusoidal Nature of SHM and its Graphical Representation:

The above equations demonstrate that SHM is in fact a sinusoidal motion. When displacement, velocity or acceleration is graphed against time, you obtain a nice curve which resembles a wave. This is so because the motion involves angles which are measured by sine or cosine functions.

A representation that can explain this quite well is that of a ball placed on a spring. When you pull the ball down and release it, it moves up and down in a swinging motion. The displacement, velocity and acceleration of the ball vary with time and these variations possess sinusoidal characteristics. This is SHM – a harmony between two forces that are in constant motion and can be described by some pleasing mathematical formulas.

Relationship between Angular Frequency and Period:

Angular frequency ω and period T are reciprocal of each other in nature and hence they are said to be closely related to each other. ω = 2πf = 2π/T. From this we can deduce that the higher the value of oscillation (frequency), the low the value of the period and vise versa. Similar to a tightrope walker, the quicker it is done and thus less time is taken in one cycle.

Energy Considerations in SHM

• Kinetic Energy and Potential Energy:

In SHM there is an exchange of kinetic energy (KE) and potential energy (PE).

Kinetic Energy (KE): 

The energy associated with its motion. While the object moves to and fro, it moves at a different rate of speed and, therefore, its KE is different.

Potential Energy (PE): 

The energy of position. In the spring mass system, potential energy is located at the elongated or compressed spring. In a pendulum for example, PE is determined by point of pendulum’s height relative to the midline of the swing.

• Conservation of Mechanical Energy in SHM:

It is important to note if there is no friction or other forces for dissipation the total energy of the mass (KE + PE) remains constant in SHM. This implies that at any given stage of the oscillation of the object, the total energy given by KE plus PE is conserved.

Consider it as a see-saw – one side rises while the other side fall, the energy in the see-saw does not change. Likewise in SHM, KE and PE are inversely proportional to each other but the sum of the two will always be a constant.

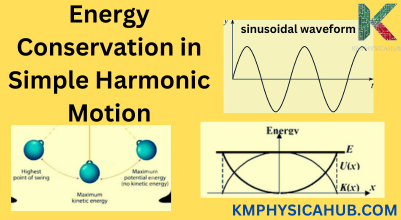
Energy Transfer between Kinetic and Potential Energy:

At the equilibrium point, the object experiences the highest kinetic energy and the least potential energy. As it gets further away from the equilibrium position, the KE decreases, but the PE increases simultaneously. At the maximum displacement, the object has maximum potential energy and minimum kinetic energy. This exchange of energy between KE and PE is happening continuously, and is one of the characteristics of SHM.

Applications of SHM

• Resonance:

Definition of Resonance: 

Resonance is the tendency of a system to oscillate with increasing amplitude when subjected to an external force at its natural frequency. The natural frequency is the frequency that the system use when undergoing free vibration. Whenever the driving frequency corresponds with the natural frequency of the system, energy is effectively absorbed and the amplitude of the oscillation increases dramatically.

Explanation of How Resonance Occurs: 

Consider the act of gently nudging a child on a swing. If an external force is applied at the natural frequency of the swing, the size of the swing will grow with each push. You are contributing energy into the system, in the most optimal fashion.

Examples of Resonance:

A Swing: When one pushes a swing at a given natural frequency, the swing is pushed higher and higher.

A Tuning Fork: When the tuning fork is hit, it starts to oscillate at one of its characteristic frequencies. If you take another tuning fork that has nearly the same natural frequency as the first one, the second tuning fork will also begin to oscillate as a result of resonance.

A Bridge: It is also important to know that bridges oscillate on a natural frequency. If winds blow at this frequency, the bridge could vibrate and possibly bring down the structure.

A Musical Instrument: Most musical instruments work by resonating sound. The strings or the air columns in an instrument are made to vibrate at some particular frequencies. When you play a note, the frequencies of the instrument gets excited and it begins to vibrate and amplify the sound.

• Applications in Music, Engineering, and Other Fields:

Musical Instruments:

• String Instruments: 

The strings of guitar, violin, piano, and several other musical instruments oscillate in SHM when played. Frequency of the vibration defines the note played by the instrument. Musicians are able to change the tension or length of the string and produce different frequency, or notes.

• Wind Instruments: 

In wind instruments such as flutes, trumpets, and clarinets, the column of air enclosed in them oscillate in SHM and produces the sound waves. This is done by varying the length of the air column with the help of valves or keys, thereby altering the frequency and hence the notes produced.

• Percussion Instruments: 

The vibrating surfaces of drums and cymbals also illustrate SHM. The frequency of vibrations is dependent on the dimensions of the instruments and the type of materials used to make the instruments.  This leads to variation in pitch and quality.

Engineering:

• Structural Design: 

Engineers apply the principles of SHM in developing civil structures such as the bridge, buildings and airplanes that can sustain the vibration and oscillation. Knowledge of the natural frequencies is important to avoid resonance and possible catastrophic failures of the structures.

• Machine Design: 

Most of the machines such as engines and turbines have parts that undergo SHM. These oscillations must be endured by the components and engineers have to design the same in such a manner that they do not fail.

• Shock Absorbers: 

Most vehicles come fitted with shock absorbers which are supposed to control the oscillation of the suspensions for a smoother ride. They employ damped SHM principles whereby the energy from vibrations resulting from movement on the bump and other uneven surface is dissipated.

• Other Fields:

Electronics: 

An important usage of SHM is in electronic circuits, especially in oscillators that produce periodic signals. These oscillators are widely used in electronic equipment such as clocks, radios and other similar gadgets.

Seismology: 

Seismic analysis depends on knowledge of SHM. Another example of a wave structure that possesses the properties of SHM is seismic waves that travel through the Earth’s crust. From this knowledge, seismologists are able to extract more earthquake data and forecast future seismic activities.

Medicine: 

SHM can be used in other medical imaging processes like ultrasound. Ultrasound waves are sound waves that operate on frequencies that are higher than the audible range and are used to form images of internal organs and tissues. These waves pass through the body in a fashion similar to SHM, and they can be used to diagnose and treat many different diseases.

Damped and Forced Oscillations

The effects of damping on SHM:

Real-life oscillations are usually bounded by frictional forces, which can act to damp the vibrations. This therefore implies that in an oscillation, the amplitude diminish over time to the point of no oscillation.

Imagine a swinging clock’s pendulum that goes back and forth. The air resistance and friction from the pivot point will gradually decelerate the pendulum until it ceases to move. This is damping.

Forced Oscillations and Resonance:

Forced oscillations are a result of the application of a periodic force to the system. This means that the frequency of the force that is being applied can be different to that of the system natural frequency.

It’s just like pushing a child on a swing but instead of pushing at the frequency of the swing that the child has, you push at a different one. The oscillation will continue, but it will be in a manner such that the amplitude is less than the amplitude that results when you push at the natural frequency of the swing.

Examples of Damped and Forced Oscillations:

Following are some real-world examples of damped and forced oscillations:

Shock absorbers in cars: 

Suspension systems include shock absorbers whose function is to minimize the vibrations of the car’s suspending system.

Earthquake-resistant buildings: 

To reduce the impact of the earthquake,  structures are designed in such a way that they have damping systems which reduce the energy of the seismic waves.

Conclusion:

Simple harmonic motion is an important part of the study of physics where objects move back and forth in a periodic fashion due to a force that is directly proportional to the displacement from an equilibrium position. It is characterized by its sinusoidal nature, the fact that mechanical energy is conserved in the process, and employs multiple uses.

SHM is found in all forms of oscillations of springs, pendulums, sound and light waves, right down to the atomic levels, among others. It offers a strong theoretical and conceptual foundation for explaining and modeling such phenomena.

The analysis of SHM remains an active field of development, with new perspectives arising from quantum mechanics and nonlinear dynamics. Thus, enhanced comprehension of SHM can open new prospects in the exploration of the Universe and the invention of new technologies.

FAQs

Q1. Give some real-world examples of SHM.

A: Examples include:

1.     Pendulums
2.     Mass-spring systems
3.     Musical instruments
4.     Seismic waves
5.     Ultrasound imaging

Q2. How does damping affect SHM?

A: Damping is the act of reducing the amplitude of oscillations by dissipation of energy through friction or other resisting forces.

Q3. Can SHM exist without a restoring force?

A: No. SHM is actually defined by the presence of a restoring force, which seeks to bring the object back into equilibrium. In the absence of this force the motion is not oscillatory and therefore cannot be classified as Simple Harmonic Motion.

Q4. How does the amplitude of SHM affect the energy of the system?

A: The energy stored in SHM is directly proportional to the square of the amplitude of oscillation. This means that when a wave’s amplitude is doubled the energy of the system increases four fold.

Q5. Can two SHM systems with different frequencies interact?

A: Yes, they can interact, producing phenomena such as beats and superposition. Beats occur when the frequencies are slightly different causing oscillation of the amplitudes. Superposition enables one to add two or more SHMs in order to produce a new waveform.